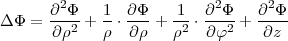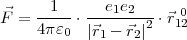
Gegenstand:
e = 1,6 ⋅ 10-19As (Elektrolyse, Millikan-Versuch)
Kraft zwischen zwei Punktladungen:
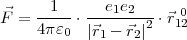
mit

Ladungseinheit: 1As = 1C
Jede einzelne Ladung q erzeugt einen Zustand des Raumes, den man elektrisches Feld dieser Ladung nennt.
Definition: 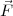 ≡ q′
≡ q′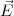 (wobei q′ klein,
ruhend)
(wobei q′ klein,
ruhend)
Das elektrische Feld wird definiert über eine Kraft auf eine ruhende Probeladung (mit verschwindend kleiner Ladung limq′→ 0)
Beispiel: el. Feld einer Punktladung q am Orte r1

speziell: Ladung q im Ursprung, 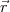 1 =
1 =  und Aufpunkt
und Aufpunkt 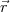 2 =
2 = 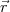
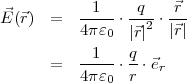
Mit |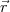 | = r, wobei
| = r, wobei 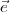 r der Einheitsvektor in radialer Richtung ist.
r der Einheitsvektor in radialer Richtung ist.
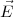 (
( ) ist ein Vektorfeld!
) ist ein Vektorfeld!
Grundproblem der Elektrostatik:
Gegeben sind ruhende Ladungen (oder Ladungsverteilungen), welches elektrische Feld stellt sich ein?
Für Punktladungen ist das Problem gelöst.
Am Orte  n : qn N Stück
n : qn N Stück
Kräfte auf q′ bei  addieren sich: Superposition der Felder!
addieren sich: Superposition der Felder!
für kontinuierliche Ladungsverteilungen:

Dabei ist dV ′ = dx′dz′dy′.
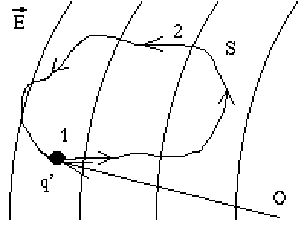
Es sei ein elektrisches Feld gegeben, in dem sich die Probeladung q′ befindet:
 (
(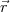 ) = q′⋅
) = q′⋅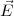 (
(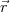 ) Arbeit bei Abschreiten des Weges C:
) Arbeit bei Abschreiten des Weges C:
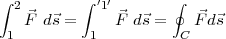
wegen Energieerhaltung, es hat sich beim Durchlaufen des Wegs nichts geändert!
Reminiszenz an Mechanik:
Ein konservatives Kraftfeld ist ein Vektoreld mit der Eigenschaft ∮
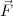 ⋅d
⋅d = 0 für jeden geschlossenen
Weg.
= 0 für jeden geschlossenen
Weg.
Diese Aussage ist äquivalent mit:
Es existert eine skalare Funktion ϕ( ) mit
) mit
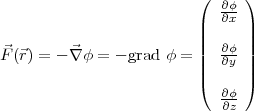
Hier ist 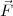 (
( ) = q ⋅
) = q ⋅ (
(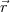 )
)
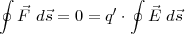
d.h.:
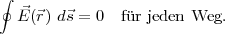
⇔∃ skalare Funktion Φ( ) mit
) mit
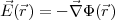
Die skalare Funktion Φ heißt elektrostatisches Potential.


In der Elektrostatik ist:
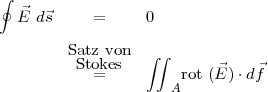
Wiederholung:

⇒ 
1. Maxwellgleichung der Elektrostatik
Beispiel:
Punktladung
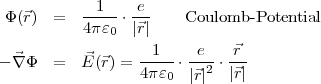
Ladungsverteilung
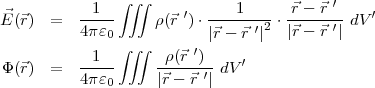
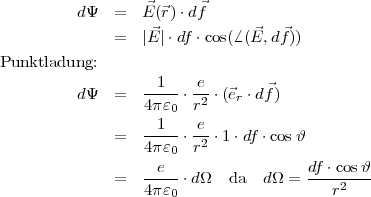
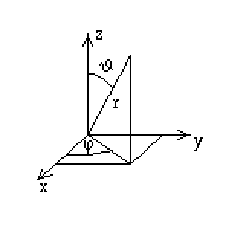
In sphärischen Polarkoordinaten: dΩ = sin(ϑ) dϑ dφ
Für eine endlich Fläche gilt somit Ψ = 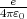 Ω,
Ω,
insbesondere gilt für eine eingeschlossene Ladung:
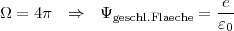
viele Ladungen:
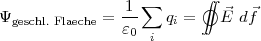
Ladungen außerhalb der geschlossenen Fläche liefern keinen Beitrag zum elektrischen Kraftfluss, er kompensiert sich bei Ein- und Austreten der Feldlinien ⇒ Verallgemeinerung:
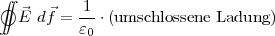
Für kontinuierliche Ladungsverteilungen ρ( ′) gilt:
′) gilt:

(Hier wird über das von der Fläche eingeschlossene Volumen integeriert)
Satz von Gauß:
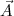 (
(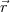 ) ist ein Vektorfeld, O(V) ist die Oberfläche des Volumens V.
) ist ein Vektorfeld, O(V) ist die Oberfläche des Volumens V.
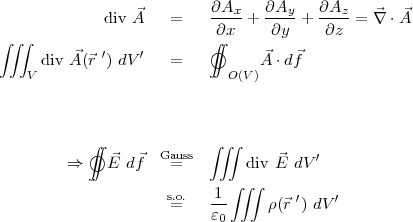
Da dies für beliebige Flächen gilt, folgt daraus:
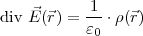
2. Maxwellgleichung der Elektrostatik
Mit 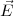 = -
= -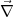 Φ ⇒
Φ ⇒ 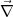
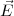 = -
= -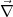 ⋅
⋅ ⋅ Φ = -ΔΦ
⋅ Φ = -ΔΦ
erhält die 2. Maxwellgleichung damit die Gestalt:
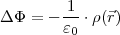
Poissongleichung
Sind keine Ladungen vorhanden, hat man also ρ(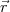 ) = 0, erhält man:
) = 0, erhält man:
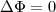
Laplacegleichung
Wiederholung:
Gestalten des Laplace-Operators:
karthesische Koorrdinaten: (x,y,z)
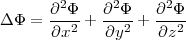
sphärische Polarkoordinaten: (r,ϑ,φ)
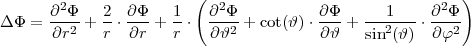
Zylinderkoordinaten: (ρ,φ,z)